2021年2月2日
ZephyrとQEMUのリセット その1 - 準備編
目次: Zephyr
Zephyrでリセットできないんだけど、って言われて調べたので、忘れないうちに記録に残しておきます。
RISC-Vの規格ではリセット処理について何も記述されていませんので、リセット処理はハードウェア依存となります。QEMUのRISC-V virtマシンはどうかというと、SiFiveのナイスガイ達が作ってくれたリセットの仕組みがあります。
QEMU RISC-V virtマシンのリセット処理
// qemu/hw/riscv/virt.c
static const struct MemmapEntry {
hwaddr base;
hwaddr size;
} virt_memmap[] = {
[VIRT_DEBUG] = { 0x0, 0x100 },
[VIRT_MROM] = { 0x1000, 0xf000 },
[VIRT_TEST] = { 0x100000, 0x1000 }, //★アドレス0x00100000にある★
[VIRT_RTC] = { 0x101000, 0x1000 },
...
// qemu/hw/riscv/virt.c
static void virt_machine_init(MachineState *machine)
{
...
/* SiFive Test MMIO device */
sifive_test_create(memmap[VIRT_TEST].base); //★テストデバイスを追加している★
// qemu/hw/misc/sifive_test.c
/*
* Create Test device.
*/
DeviceState *sifive_test_create(hwaddr addr)
{
DeviceState *dev = qdev_new(TYPE_SIFIVE_TEST);
sysbus_realize_and_unref(SYS_BUS_DEVICE(dev), &error_fatal);
sysbus_mmio_map(SYS_BUS_DEVICE(dev), 0, addr);
return dev;
}
...
static void sifive_test_write(void *opaque, hwaddr addr,
uint64_t val64, unsigned int size)
{
if (addr == 0) {
int status = val64 & 0xffff;
int code = (val64 >> 16) & 0xffff;
switch (status) {
case FINISHER_FAIL:
exit(code);
case FINISHER_PASS:
exit(0);
case FINISHER_RESET:
qemu_system_reset_request(SHUTDOWN_CAUSE_GUEST_RESET); //★ここに到達するとリセットが掛かるはず★
return;
default:
break;
}
}
qemu_log_mask(LOG_GUEST_ERROR, "%s: write: addr=0x%x val=0x%016" PRIx64 "\n",
__func__, (int)addr, val64);
}
// qemu/include/hw/misc/sifive_test.h
enum {
FINISHER_FAIL = 0x3333,
FINISHER_PASS = 0x5555,
FINISHER_RESET = 0x7777 //★この値を書けば良さそう★
};
つまり0x100000に0x00007777を4バイトWriteすれば良さそうです。
準備
Zephyrのサンプルshellを使います。理由はリブートするコマンドが簡単に使えるからです。CONFIG_REBOOTを有効にする必要があります。またshellは起動後プロンプトが出るだけで、リセットが掛かったかどうかわかりにくいため、起動時のバナーも有効にしておくと良いです。
REBOOT, BOOT_BANNERを有効にする
CONFIG_REBOOT=y
Boot Options --->
[ ] Reboot functionality
CONFIG_BOOT_BANNER=y
General Kernel Options --->
Kernel Debugging and Metrics --->
[ ] Boot banner
ちょっと長いので一旦切ります。次回は実装と動作確認をします。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月3日
ZephyrとQEMUのリセット その2 - 実装編
目次: Zephyr
Zephyrにはリブートを行う関数sys_reboot() が既に実装されており、アーキテクチャごとのリブート用関数sys_arch_reboot() を呼ぶ仕組みです。
QEMU RISC-V virtマシンのリブート処理を実装
// zephyr/subsys/power/reboot.c
void sys_reboot(int type)
{
(void)irq_lock();
#ifdef CONFIG_SYS_CLOCK_EXISTS
sys_clock_disable();
#endif
sys_arch_reboot(type); //★★アーキテクチャごとのリブート関数を呼ぶ
/* should never get here */
printk("Failed to reboot: spinning endlessly...\n");
for (;;) {
k_cpu_idle();
}
}
// zephyr/soc/riscv/riscv-privilege/virt/soc.c
/* Reboot machine */
#define FINISHER_REBOOT 0x7777
void sys_arch_reboot(int type)
{
volatile uint32_t *reg = (uint32_t *)SIFIVE_SYSCON_TEST;
*reg = FINISHER_REBOOT; //★★0x100000に0x00007777をWrite
ARG_UNUSED(type);
}
// zephyr/soc/riscv/riscv-privilege/virt/soc.h
#include <soc_common.h>
#include <devicetree.h>
#define SIFIVE_SYSCON_TEST 0x00100000 //★追加
#define RISCV_MTIME_BASE 0x0200BFF8
#define RISCV_MTIMECMP_BASE 0x02004000
実装は素直にsys_arch_reboot() を追加しただけです。そんなに難しくないですよね。
動作確認
前回説明した通り、サンプルアプリのshellを使って動作確認します。
リブートの動作確認
$ cmake -G Ninja -DBOARD=qemu_riscv32 ../samples/subsys/shell/shell_module/ $ ninja menuconfig ★★CONFIG_REBOOTとCONFIG_BOOT_BANNERを有効にする $ ninja run [0/1] To exit from QEMU enter: 'CTRL+a, x'[QEMU] CPU: riscv32 *** Booting Zephyr OS build v2.5.0-rc1-276-ge7d3bb714bc2 *** uart:~$ kernel reboot cold ★★↑ここでリブートされる *** Booting Zephyr OS build v2.5.0-rc1-276-ge7d3bb714bc2 *** uart:~$
無事リブートしました。本当にリブートしてるのか不安になるくらい速いです。Zephyrは起動時に何も言わないので、Linuxと比べるとリブートは簡素に見えますね。速いのは良いんだけど、感動がちょっと薄いのが難点かも?
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月4日
不安定なyes
目次: ベンチマーク
昔(2017年6月14日の日記参照)yesの速度を測ったりして遊んでいましたが、改めてRyzen 7 2700でyes | pv > /dev/nullを実行してみたところ、出力速度が不安定です。
- GNU yes 8.32を単独で実行
- [6.73GiB/s](不安定)
- GNU yes 8.32と、隣でwhile :; do :; doneを実行
- [6.98GiB/s](若干安定)
出力速度が不安定なときに、topで各CPUスレッドの負荷を眺めていると、ときどきプロセスが違うCPUスレッドに移動しているようにみえます。コアごとに動作周波数が違うせいか、yesのプロセスが別のコアに移ったとき、移動先のコアが省エネモードから最高周波数に立ち上がるまでのラグが影響しているんでしょうか?どうやって確かめましょうね?特定のスレッドに貼り付けたらエエんかしら??
てなことを最初考えたんですが、実はそんなに難しい話ではなく、単にyesとpvが同じコアに割り付けられたときに、速度的に不利に働いているだけのような気がしてきました。実験するためtasksetを使って適当にスレッドを散らします。
- 隣のスレッド(= 同じコア)
- $ taskset 0x2 yes | taskset 0x1 pv > /dev/null
[6.34GiB/s] - 2つ隣のスレッド(= 違うコア、コアコンプレックス内)
- $ taskset 0x4 yes | taskset 0x1 pv > /dev/null
[7.34GiB/s] - 4つ隣のスレッド(= 違うコア、コアコンプレックス内)
- $ taskset 0x10 yes | taskset 0x1 pv > /dev/null
[7.20GiB/s] - 8つ隣のスレッド(= 違うコア、コアコンプレックス外)
- $ taskset 0x100 yes | taskset 0x1 pv > /dev/null
[4.65GiB/s] - 12つ隣のスレッド(= 違うコア、コアコンプレックス外)
- $ taskset 0x1000 yes | taskset 0x1 pv > /dev/null
[4.66GiB/s]
かなり性能が変わります。コアが同じかどうか?はもちろん重要ですが、Zenアーキテクチャはコアコンプレックスの内か外かで性能に大きな違いが出ます。結果が安定しなかったのはプロセスがコアコンプレックス外に行ったり来たりしていたためでしょうね。
Debian TestingのLinux Kernel(現状、5.10.4-1)は、コアコンプレックスまでは考慮してくれないらしく、コアコンプレックス内と外のコアのどちらで実行しても良いよ、という設定にすると、処理が遅くなる方に割り付けてしまいます。
実行中のtopの様子
$ taskset 0x110 yes | taskset 0x1 pv > /dev/null [4.59GiB/s] $ top top - 02:05:53 up 16 days, 9:39, 20 users, load average: 0.64, 0.96, 1.06 Tasks: 355 total, 3 running, 349 sleeping, 2 stopped, 1 zombie %Cpu0 : 7.5 us, 75.8 sy, 0.0 ni, 16.7 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st ★pvはCPU 0で動作する %Cpu1 : 0.0 us, 0.0 sy, 0.0 ni,100.0 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu2 : 0.3 us, 0.3 sy, 0.0 ni, 99.3 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu3 : 0.3 us, 0.3 sy, 0.0 ni, 99.3 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu4 : 0.0 us, 0.3 sy, 0.0 ni, 99.7 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu5 : 0.0 us, 0.0 sy, 0.0 ni,100.0 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu6 : 0.0 us, 0.3 sy, 0.0 ni, 99.7 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu7 : 0.3 us, 0.0 sy, 0.0 ni, 99.7 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu8 : 6.0 us, 79.1 sy, 0.0 ni, 14.9 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st ★yesはCPU 4のほうが速いはずだが、CPU 8で動作する %Cpu9 : 0.0 us, 0.0 sy, 0.0 ni,100.0 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu10 : 0.7 us, 0.0 sy, 0.0 ni, 99.3 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu11 : 0.3 us, 0.0 sy, 0.0 ni, 99.7 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu12 : 0.3 us, 0.3 sy, 0.0 ni, 99.3 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu13 : 0.0 us, 0.0 sy, 0.0 ni,100.0 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu14 : 0.7 us, 0.3 sy, 0.0 ni, 99.0 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st %Cpu15 : 0.0 us, 0.3 sy, 0.0 ni, 99.7 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st MiB Mem : 32106.7 total, 582.9 free, 3532.5 used, 27991.3 buff/cache MiB Swap: 0.0 total, 0.0 free, 0.0 used. 27906.8 avail Mem
パッと見、法則性が良くわかりませんでした。なるべくビジーなスレッドから遠い番号のCPUスレッドに割り当てようとする?のかもしれませんね。
(※1)Ryzen 7は1コア2スレッドなので、スレッド (0, 1), (2, 3), (4, 5) のように2スレッドが同じコアで実行されます。
メモ: 技術系?の話はFacebookから転記しておくことにした。後半を加筆。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月5日
デノーマルフラッシュ
目次: ベンチマーク
浮動小数点数の演算ではIEEE 754という規格があり、x86系のプロセッサはこの規格に基づいた演算を行っています。規格のなかに非正規化数(Denormal NumberもしくはSubnormal Numberとも)という、極めて小さい特殊な数のカテゴリがあります(参考: IEEE 754 - Wikipedia)。
通常はDenormal数も正確に演算しますが、Denormal数の演算は遅いです。計算精度より計算速度が重要な場面ではMXCSRレジスタに特殊なフラグを設定することで、Denormal数の扱いを変更し、高速に演算することができます(参考: FTZフラグとDAZフラグの設定 - インテルC++ コンパイラー18.0デベロッパー・ガイドおよびリファレンス)。
基本的にはDenormal数を無視して0として扱うようにしますが、Intelのプロセッサでは入力側と出力側を別々に扱えるようです。設定可能なフラグは2つあります。デノーマルフラッシュって必殺技の名前っぽいよね。どうでもいいけど。
- FTZ (Flush To Zero)
- 演算結果がDenormal数だった場合、ゼロとして扱う。
有効にする方法 _MM_SET_FLUSH_ZERO_MODE(_MM_FLUSH_ZERO_ON) - DAZ (Denormals Are Zeros)
- 入力がDenormal数だった場合、ゼロとして扱う。
有効にする方法 _MM_SET_DENORMALS_ZERO_MODE(_MM_DENORMALS_ZERO_ON)
うーん。わかるような、わからないような。こういうときは実際に動かしてどんな結果になるか試すのが一番良いでしょう。FTZとDAZを有効にする方法はIntelコンパイラの説明から抜粋したものですが、GCCでも全く同じ方法で利用可能です。
Denormal Flushの実験プログラム
#include <stdint.h>
#include <stdio.h>
#include <pmmintrin.h>
double zero = 0.0f;
union {
double f;
long long n;
} a, b, c, d, ab, ac, ca, dc;
void test()
{
a.n = 0x0008000000000000ULL;
b.n = 0x0004000000000000ULL;
c.n = 0x0010000000000000ULL;
d.n = 0x0014000000000000ULL;
ab.f = a.f + b.f;
ac.f = a.f + c.f;
ca.f = c.f - a.f;
dc.f = d.f - c.f;
printf(" a : %e(0x%08llx)\n"
" b : %e(0x%08llx)\n"
" c : %e(0x%08llx)\n"
" d : %e(0x%08llx)\n"
" a+b : %e(0x%08llx)\n"
" a+c : %e(0x%08llx)\n"
" c-a : %e(0x%08llx)\n"
" d-c : %e(0x%08llx)\n"
" a==0: %d\n\n",
a.f, a.n, b.f, b.n, c.f, c.n, d.f, d.n,
ab.f, ab.n, ac.f, ac.n, ca.f, ca.n, dc.f, dc.n,
a.f == zero);
}
int main(int argc, char *argv[])
{
_MM_SET_FLUSH_ZERO_MODE(_MM_FLUSH_ZERO_OFF);
_MM_SET_DENORMALS_ZERO_MODE(_MM_DENORMALS_ZERO_OFF);
printf("FTZ:OFF, DAZ:OFF\n");
test();
_MM_SET_FLUSH_ZERO_MODE(_MM_FLUSH_ZERO_OFF);
_MM_SET_DENORMALS_ZERO_MODE(_MM_DENORMALS_ZERO_ON);
printf("FTZ:OFF, DAZ:ON\n");
test();
_MM_SET_FLUSH_ZERO_MODE(_MM_FLUSH_ZERO_ON);
_MM_SET_DENORMALS_ZERO_MODE(_MM_DENORMALS_ZERO_OFF);
printf("FTZ:ON, DAZ:OFF\n");
test();
_MM_SET_FLUSH_ZERO_MODE(_MM_FLUSH_ZERO_ON);
_MM_SET_DENORMALS_ZERO_MODE(_MM_DENORMALS_ZERO_ON);
printf("FTZ:ON, DAZ:ON\n");
test();
return 0;
}
変数aとbはDenormal数です(doubleのexponent部分が0)。変数cは非常に小さいですが通常の数です。最後のa.f == zeroはDenormal数と0を比較したときに、等しければ1、等しくなければ0が出力されます。実行結果とともに説明したほうが良いと思うので、実行結果を示します。
Denormal Flushの動作確認
$ gcc a.c && ./a.out FTZ:OFF, DAZ:OFF a : 1.112537e-308(0x8000000000000) b : 5.562685e-309(0x4000000000000) c : 2.225074e-308(0x10000000000000) d : 2.781342e-308(0x14000000000000) a+b : 1.668805e-308(0xc000000000000) ★Denorm1 + Denorm2 = Denorm3 a+c : 3.337611e-308(0x18000000000000) ★Denorm1 + Normal1 = Normal1+α c-a : 1.112537e-308(0x8000000000000) ★Normal1 - Denorm1 = Denorm4 d-c : 5.562685e-309(0x4000000000000) ★Normal2 - Normal1 = Denorm5 a==0: 0 ★Denorm1 == 0 ? いいえ FTZ:OFF, DAZ:ON a : 1.112537e-308(0x8000000000000) b : 5.562685e-309(0x4000000000000) c : 2.225074e-308(0x10000000000000) d : 2.781342e-308(0x14000000000000) a+b : 0.000000e+00(0x00000000) ★Denorm1 + Denorm2 = 0(※1) a+c : 2.225074e-308(0x10000000000000) ★Denorm1 + Normal1 = Normal1 → 入力のDenormalが0扱い = DAZ c-a : 2.225074e-308(0x10000000000000) ★Normal1 - Denorm1 = Normal1 → 入力のDenormalが0扱い = DAZ d-c : 5.562685e-309(0x4000000000000) ★Normal2 - Normal1 = Denorm5 a==0: 1 ★Denorm1 == 0 ? はい → 入力のDenormalが0扱い = DAZ FTZ:ON, DAZ:OFF a : 1.112537e-308(0x8000000000000) b : 5.562685e-309(0x4000000000000) c : 2.225074e-308(0x10000000000000) d : 2.781342e-308(0x14000000000000) a+b : 0.000000e+00(0x00000000) ★Denorm1 + Denorm2 = 0(※1) a+c : 3.337611e-308(0x18000000000000) ★Denorm1 + Normal1 = Normal1+α c-a : 0.000000e+00(0x00000000) ★Normal1 - Denorm1 = 0 → 演算結果のDenormalが0扱い = FTZ d-c : 0.000000e+00(0x00000000) ★Normal2 - Normal1 = 0 → 演算結果のDenormalが0扱い = FTZ a==0: 0 ★Denorm1 == 0 ? いいえ FTZ:ON, DAZ:ON a : 1.112537e-308(0x8000000000000) b : 5.562685e-309(0x4000000000000) c : 2.225074e-308(0x10000000000000) d : 2.781342e-308(0x14000000000000) a+b : 0.000000e+00(0x00000000) ★Denorm1 + Denorm2 = 0(※1) a+c : 2.225074e-308(0x10000000000000) ★Denorm1 + Normal1 = Normal1 → 入力のDenormalが0扱い = DAZ c-a : 2.225074e-308(0x10000000000000) ★Normal1 - Denorm1 = Normal1 → 入力のDenormalが0扱い = DAZ d-c : 0.000000e+00(0x00000000) ★Normal2 - Normal1 = 0 → 演算結果のDenormalが0扱い = FTZ a==0: 1 ★Denorm1 == 0 ? はい → 入力のDenormalが0扱い = DAZ (※1)演算結果だけでは、入力のDenormal数が両方0扱いなのか、結果のDenormal数が0扱いなのか、判別できない。
FTZとDAZが発生する例を示したつもりです。できるだけ頑張って説明してみたんですが、良くわからなかったらごめんなさい。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月6日
レガシィの半年点検
目次: 車
ディーラーから電話がかかってきて「(車検と一緒にセットで頼んだ)半年点検どうしましょうか?」と聞かれました。実は頼んだことを忘れていたので、確認してもらって助かりました。「半年前の車検で一緒にご依頼されました半年点検なんですが〜」と説明が妙に手慣れた感じだったところを見るに、頼んでおいて忘れてしまう、私みたいな人が多いんだな〜なんて思った。
点検結果はというと、走行系の異常はありませんでした。フロントのウォッシャー液を送るゴムホースが破損していて、フロントのウォッシャー液が出ないうえ、むりやり使ったらエンジンルームにダダ漏れするそうです。え、そうなの??全く気づいていませんでした。ウォッシャー液って全然使わないんだよね……。
部品の取り寄せが要るためすぐには直せず、修理の際はご予約いただきたい、とのことだったので、またどこかの土曜日にでも持っていこうと思います。
スバルのセダンは1つだけ
私のようなおじさんがディーラーに行くと、新車のカタログをたくさん渡されて「新車どうです?」って話されるんですが、最近のスバルではなーんにも聞かれません。今のスバルはレガシィB4 GTの乗り換え先がないからです。
スバルの現行車種でセダンはインプレッサG4だけです。G4は上級グレードの2.0iでも、2リッターNA(154馬力)です。レガシィB4 GTの2リッターターボ(280馬力)から乗り換えると大幅パワーダウンは否めず、おすすめしづらいのでしょう。現にディーラーでもカタログだけもらったものの、ほとんどプッシュされませんでした。
ちょっと前なら、インプレッサWRX S4 STI Sportがありましたが、生産終了してしまいました。仮に現行車種だったとしても、一般人向けとは思えんし、気軽に「WRX S4いかがですか?」とは言いにくいでしょう。スバルのディーラーにとってセダン乗りは鬼門ですね。
コメント一覧
- hdkさん(2021/02/13 08:17)
トヨタのディーラーではときどき聞かれます。まぁハッチバックコンパクトカーというジャンルなので確かに車種は豊富なんですが、4人乗り全長3000mmの新車は他社を含めてももう1台もないのに... - すずきさん(2021/02/13 15:13)
そこまで珍しいと、売る側としてももう諦めて……って感じでしょうね。
 この記事にコメントする
この記事にコメントする
2021年2月8日
民主主義と人口ピラミッド
最近の日本やら先進国やらの迷走を見ていると、民主主義って人口ピラミッドが逆転することを考慮できていないのでは?と疑問を感じます。
人口ピラミッドが逆転して高齢世代が主流派になると、
- 人数少の若年世代は支援しない
- 人数多の高齢世代は支援する
このような政策が支持されるので、少子化はさらに加速し、先のない高齢世代に最大投資しまくる、まさに今の日本みたいな状態になります。当然ながら経済力は下がる一方ですし、滅亡一直線の国家です。
民主主義のバグとしか思えないですね……。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月11日
デノーマルフラッシュの速度改善効果
目次: ベンチマーク
先日(2021年2月5日の日記参照)非正規化数(Denormal数)の計算は遅いと書きましたが、いかほどでしょうか?どのくらい遅いのか、デノーマルフラッシュでどの程度速くなるのか、この2点について見ていこうと思います。
おそらく世の中のどのFPUも割り算が一番苦手なはずです。入力を正規化数、非正規化数の2パターン用意して、下記の演算をたくさん実行してみます。
浮動小数点の割り算の速度を測るためのコード(中心部分)
#define SIZE 10000
union uuu {
double f;
long long n;
};
...
void test_speed(union uuu *val)
{
for (int i = 0; i < SIZE; i++) {
dst[i].f =
val[i].f / 1.08f -
val[i].f / 1.07f +
val[i].f / 1.06f -
val[i].f / 1.05f +
val[i].f / 1.04f -
val[i].f / 1.03f +
val[i].f / 1.02f -
val[i].f / 1.01f;
}
}
コードは全部貼り付けると邪魔くさいのでGitHubにおきました(GitHubへのリンク)。前回のFTZ, DAZのテストに使ったコードも一緒に入っています。
x86系のCPU
まずはx86系のCPUで測ってみましょう。手元にあるのはZen系(AMD Ryzen 7 2700)と、Atom系(Intel Pentium J4205)なので、この2つで測ります。コンパイラはgcc (Debian 10.2.1-6) 10.2.1 20210110、最適化レベルはO2です。
Ryzen 7 2700の結果(Linux 5.10.9-1)
10000 loops Normal ----- FTZ:OFF, DAZ:OFF 0.912859[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) FTZ:OFF, DAZ:ON 0.880695[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) FTZ:ON, DAZ:OFF 0.880633[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) FTZ:ON, DAZ:ON 0.880653[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) Denormal ----- FTZ:OFF, DAZ:OFF 1.806291[s] dst : -4.446591e-323(0x8000000000000009) FTZ:OFF, DAZ:ON 0.783578[s] dst : 0.000000e+00(0x00000000) FTZ:ON, DAZ:OFF 1.513203[s] dst : 0.000000e+00(0x00000000) FTZ:ON, DAZ:ON 0.783183[s] dst : 0.000000e+00(0x00000000)
Pentium J4205の結果(Linux 5.4.95)
1000 loops Normal ----- FTZ:OFF, DAZ:OFF 1.024671[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) FTZ:OFF, DAZ:ON 1.025767[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) FTZ:ON, DAZ:OFF 1.025151[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) FTZ:ON, DAZ:ON 1.027414[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) Denormal ----- FTZ:OFF, DAZ:OFF 12.147070[s] dst : -4.446591e-323(0x8000000000000009) FTZ:OFF, DAZ:ON 0.309857[s] dst : 0.000000e+00(0x00000000) FTZ:ON, DAZ:OFF 7.126950[s] dst : 0.000000e+00(0x00000000) FTZ:ON, DAZ:ON 0.312373[s] dst : 0.000000e+00(0x00000000)
Ryzen 7 2700でもPentium J4205でも、Denormal数が計算に出現すると遅くなりますが、J4205はその傾向が顕著で10倍くらい遅いです。FTZ, DAZをONにすると、効果覿面に速くなります。
ARM系のCPU
次にARMで測ってみましょう。手元にあるのはRK3399です。Cortex-A72とCortex-A53が混載されているので、両方で測ります。カーネルはLinux 5.11.0-rc3-next-20210113、コンパイラはgcc (Debian 8.3.0-6) 8.3.0、最適化レベルはO2です。
ARMは仕様上FTZとDAZが分かれていない(FZという両方合わせたような機能がある)ので、片方だけONにした結果はありません。
Cortex-A72の結果
$ taskset 0x10 ./a.out 10000 ... 10000 loops Normal ----- FTZ:OFF, DAZ:OFF 7.153237[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) FTZ:ON, DAZ:ON 7.118581[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) Denormal ----- FTZ:OFF, DAZ:OFF 8.008282[s] dst : -4.446591e-323(0x8000000000000009) FTZ:ON, DAZ:ON 1.779883[s] dst : 0.000000e+00(0x00000000)
Cortex-A53の結果
$ taskset 0x1 ./a.out 10000 ... 10000 loops Normal ----- FTZ:OFF, DAZ:OFF 11.693382[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) FTZ:ON, DAZ:ON 11.691307[s] dst : -3.668038e-02(0xbfa2c7c56ca81140) Denormal ----- FTZ:OFF, DAZ:OFF 12.196882[s] dst : -4.446591e-323(0x8000000000000009) FTZ:ON, DAZ:ON 11.697961[s] dst : 0.000000e+00(0x00000000)
Cortex-A72はデノーマルフラッシュの効果抜群ですが、Cortex-A53はデノーマルフラッシュによる変化はほとんどありません。どちらもARMが設計した同世代のCPUにも関わらず、速度の傾向は大きく異なります。詳細な理由はARMにしかわかりませんが、なかなか興味深い結果です。
コメント一覧
- とおりすがりさん(2022/06/21 18:08)
詳しくはわからず恐縮なのですが、
Cortex-A72, A-53 がそれぞれ big.LITTLE 構成における big, little だそうなので, Cortex-A72 のほうがちょっとリッチな回路を積んでいるのかもしれません。 - すずきさん(2022/06/22 00:20)
はい、私も同意見です。A72 はおそらくデノーマルフラッシュで遅くならないような設計の FPU なのでしょうね。
 この記事にコメントする
この記事にコメントする
2021年2月12日
在宅勤務環境改善
目次: PC
COVID-19が流行し始めた昨年2月ころ、在宅勤務が主となりました。当時の気持ちを正直に言えば「すぐ収束して、電車通勤に戻るだろう」で、完全にナメていました。在宅勤務の環境もまったく整えておらず、ダイニングテーブル、ノートPC+8インチのモバイルディスプレイでした。夕食時は邪魔だから、仕事道具をガサガサ片付ける、といった具合です。
そんなこんなで1年間やってきたものの、COVID-19の予想外の長期化、それに加えて会社方針(COVID-19が収束しようとしまいと、今後は在宅勤務)もあって、在宅勤務の環境を改善することにしました。
部屋
家には、奥さんが一昨年の在宅勤務で使っていた部屋があって、幅100cmの机と背もたれ付きのオフィスチェアがあります。そのスペースを譲ってもらうことにしました。
- 1年目: 奥さん在宅勤務、私は電車通勤
- 2年目: 2人共電車通勤
- 3年目: 奥さん電車通勤、私は在宅勤務
すっかり勤務形態が逆転しました。会社のみなさんの話を聞くと、東京の狭い家で夫婦とも在宅勤務、子供まで自粛で家に居て、全く仕事にならん……みたいな地獄化したご家庭もあるみたい。我が家も夫婦同時に在宅勤務だと、スペースの確保がちょっと大変だったと思います。交代で在宅勤務になったのは、今思えば割とラッキーだったのかな?
テーブル
ダイニングテーブルはしっかりした作りで、間違いなく家で一番上等なテーブルです。一方のダイニングチェアは年中使い続けるような椅子ではなかったらしく、1年間酷使し続けたところ、座面、背面のクッションが潰れ椅子のフレームが腰にガツガツ当たるようになりました。痛ぇよーー。
部屋を移ってスペースが広がったので、大きめのデュアルディスプレイも目指します。幅120cmの机を買い足し100cmの机は横向きに合わせL字にします。
買ったのは山善のAMDT-1260 AMDL-70という一番シンプルな天板と脚だけのテーブルです(Amazonへのリンク)。Amazonで9,000円くらいとお安いです。理由はわからないですが、山善の公式サイトには載っていないんですよね。なぜだろね?
ディスプレイ
机の幅を考えると27インチx2が載りそうです。ただし、机の奥行きがあまりない(60cm)ので、大きすぎると端が見えなくなって、かえって使いにくいです。という点を勘案して24インチx2にします。
買ったのはEIZO FlexScan EV2480です。Amazonで1台4万円くらい。デュアルディスプレイにしたので、総額8万円くらい掛かりました。非常に高価ですが、これでも中位機種なんです。ちなみに上位機種のEV2495は1台7万円します。強烈!
FlexScanは重たいのが難点(純正スタンドがめちゃ重い)ですが、変な色やら、映らないやらのトラブルは皆無で非常に快適です。以前勤めてた会社(パナソニックやソシオネクスト)でも大変お世話になりました。良いメーカーですよね。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月14日
USB Type-C DisplayPort Alternate mode
目次: PC
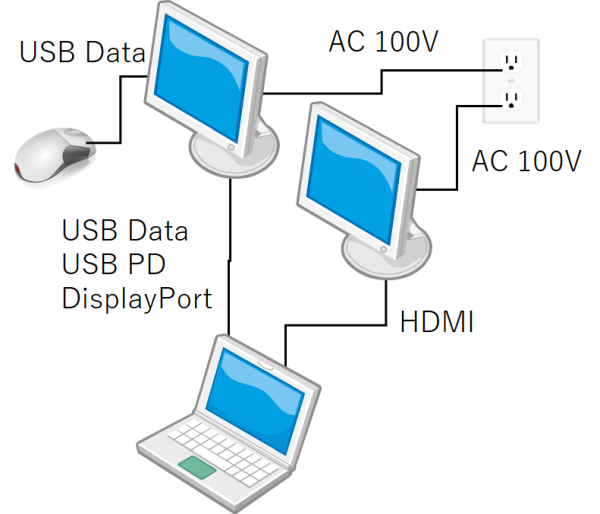
現在使っているThinkPad E480はUSB Type-C端子とHDMI端子しかありません。先日(2021年2月12日の日記参照)新しく購入したディスプレイ2つに画像を出力するには、USB Type-CのDisplayPort Alternate Mode(VESAの機能紹介のページ(英語))を使う必要があります。接続はこんな感じです。
このときE480とディスプレイを繋ぐUSB Type-Cケーブルは3つの役割を果たします。
- USB 2.0/3.1のデータ通信(ディスプレイがUSBハブになる)
- USB Power Deliveryによる電力供給
- DisplayPort Alternate Modeによる画像出力
たった1本のUSB Type-Cケーブルで3役もこなす凄いヤツです。今まで「ACアダプタ」「DisplayPort」「USB Type-A」の3つに分かれていたコネクタが、USB Type-C 1つに統合できますから、省スペースが命のノートPCにとっては大歓迎の機能でしょう。
実はさほど便利じゃない
そんな凄いヤツを使い始めて数日ですが、既に嫌になってきました。正直な感想として、少なくともユーザーからすると便利と思えないし、使わなくて良いなら使いたくないです。
- ケーブルの問題
- 1本で済むのは良いですが、ケーブルが硬すぎます。USB PD対応USB 3.1ケーブルはかなり高速な信号を通す関係上、3重シールド5〜6mm幅以上のごついケーブルばかりです。これならACアダプタとHDMI 2本の方がまだマシです。どちらもかなり細いので。
- E480の問題
- ノートPCの液晶、DisplayPort、HDMIの3系統を使えると思いきや、3画面に拡張デスクトップを設定するとバグるので、ノートPCの液晶とDisplayPortをミラーにしています。ノートPCの液晶が完全に無意味ですが、蓋を閉めるとスリープしちゃうので、半開きでテーブルの隅に放置しています。切ない。
- USBハブの問題
- ディスプレイがUSBハブの役目も果たしますが、ディスプレイの電源を切るとUSBハブとしての機能もOFFになります。マウス程度なら問題ありませんが、通信するような機器は繋ぐと毎回切られてストレスMAXです。あとUSBオーディオDACは繋いでも動作しませんでした。何か制約があるんですかね?
- USB PDの問題
- ディスプレイ側のUSB PDによる供給力の上限は、現状60Wの製品が多いです。60WはノートPCによっては給電能力がギリギリです。ディスプレイのUSB PD供給能力が足りない場合、純正アダプタに戻して給電し出画は諦めるorバッテリーを削りつつDisplayPort Altで出画するorディスプレイを買い替える、究極の3択を迫られます。
ケーブルの問題は今後、技術革新で細くなることを祈るしかありません。E480の問題は回避策不明です。HWの制約?USBハブの問題は、E480ならUSB Type-Aコネクタが別にあるので、そちらを使えば回避可能です。USB PDの問題は今の所E480だと困っていません。
しかし将来的にノートPCを買い換えるとUSB PDの問題が起きる可能性があります。回避策はあるでしょうか?USB Type-Cが3つ付いていて、1つはDisplayPort、2つ目はUSB PD電源供給、3つ目はPCに繋ぐ、変なハブ的なものがあれば良い?もはや「ケーブル1本でOK」のコンセプトは完全崩壊だし、ディスプレイ側のUSB PDは死蔵確定です。そんな訳のわからんことになるなら、素直にDisplayPortとUSB Type-Cのコネクタ2個付けてくれよって思います。
そもそもDislayPortとUSB PDなんて全く無関係のものを統合したら、どちらか壊れただけでPCが機能不全になることくらい、聡明なVESAやUSB-IFの面々には明らかなはずですけど、何でこんなデザインにしたんですかね?理解しがたいよ……。
USB PDとDisplayPort Alt Modeを見ると思い出すのは、あの商品
昔SHARP SF1という製品がありました(DIMEの記事)。スーパーファミコンとテレビが1つに合体した、当時小学生だった私には夢のような製品でした。配線なしで見た目スッキリ、場所も取らない、ACアダプタやビデオケーブルを接続する手間も不要、いかにも便利そうじゃないですか?結構お高いのもあって、友達が持っているのを見て羨ましかったです。USB Type-Cも似たような売り文句です。
しかし後から聞くところによれば、テレビが故障するとスーパーファミコンを外せないから他のテレビに繋げなくて困る、逆にスーパーファミコンが故障するとテレビごと修理になって高ぇわテレビがなくなるわで困る、元より不便になっています。元々バラバラの製品を無理やり一蓮托生にしたら、そりゃそうなりますわな……。無関係の機能をデタラメに統合してはいけない、という好例です。
残念なことにUSB Type-CもDisplayPortとUSB PDの機能統合で、似たような落とし穴に落ちています。小学生の私に「21世紀になっても人類はSF1と同じ過ちを繰り返しているよ」って教えてあげたいですね。
コメント一覧
- hdkさん(2021/02/15 06:24)
テレビデオも壊れたときがと聞いて買いませんでしたが、狭い学生宿舎で数年使えればいいだけならあれも手だったのかもとは思います。
USB Type-Cのハブは、一本させば全部つながるというのなら、外して会議室や外出先に持ち出し・戻ってつなぐ用途では楽になりそうです。同様に使えるドッキングステーションやウルトラベースもありましたよね。 - すずきさん(2021/02/15 11:27)
そうですね、1年だけとか、出張の時だけ、といった使い方にはとても便利だと思います。
今回は常用したかったので、困りました。DisplayPort Alt mode は存在していただいて構わないんですけど、代わりの機能がないところが一番困ったところです。
 この記事にコメントする
この記事にコメントする
2021年2月15日
Wikipediaの数学のページを眺める
群とか環とか体とか、大学で教えてもらった記憶がうっすらありますが、何回見ても忘れます。幸いにもWikipedia先生に割と詳しく解説されているので、まとめておこうと思います。
群
集合Gと二項演算uの組(G, u)を考えます。uは乗法や加法と呼ばれる場合があるようです。以降u(a, b) をa + bの形で表します。
- 半群
- 閉性を満たす: 二項演算u(u: G + G -> G)の結果はGに含まれる
- 結合法則を満たす: a + (b + c) = (a + b) + c
- モノイド
- 単位元eが存在する: a + e = e + a、整数の加法でいえば0
- 群
- 逆元xが存在する: a + x = x + a = e整数の加法でいえば -a
- アーベル群
- 交換法則を満たす: a + b = b + a
下にある群は、上の群の性質をすべて満たします(以降も特に断りがなければ同じ)。なので、モノイドは半群の性質を満たしますし、群はモノイドと半群の性質を満たします。
環
集合Rと2つの二項演算u, tの組(R, u, t) を考えます。(R, u) はアーベル群です。uは加法、tは乗法と呼ばれるようです。以降t(a, b) をa * bの形で表します。
- 乗法半群
- 閉性を満たす: 二項演算t(t: R * R -> R)の結果はRに含まれる
- 結合法則を満たす: a * (b * c) = (a * b) * c
- 乗法モノイド
- 単位元eが存在する: a * e = e * a、整数の乗法でいえば1
- 環(モノイドでない場合がある)
- 加法の上に左分配律を満たす: a * (b + c) = (a * b) + (a * c)
- 加法の上に右分配律を満たす: (a + b) * c = (a * c) + (b * c)
- 可換環(モノイドでない場合がある)
- 交換法則を満たす: a * b = b * a
群と違って、環はモノイド(単位元が存在する)である必要はないみたいです。
零因子
可換環では零でない零因子という困ったことが起きます。
- a * x = 0となるx != 0が存在するときaは左零因子
- y * a = 0となるy != 0が存在するときaは右零因子
困る例として挙げられていたのはa * b = 0かつa != 0でもb = 0とは限らない、もしくは、a * b = a * cかつa != 0でも、b = cとは限らない、という例でした。
具体的な例が載ってませんでしたが、行列の和と積を考えると発生しそうに思えます。
左零因子になるかな?
A = [1, 1] [0, 0] B = [ 1, 0] [-1, 0] C = [0, -1] [0, 1] A * B = [0, 0] [0, 0] A * C = [0, 0] [0, 0] A != 0だがB, Cは零行列ではない。A * B = A * Cだが、B = Cでもない。
環はこういうパターンが無数に出てきて、さらに条件を厳しくしないと困る場合がありますよ、ということですかね?
整域
変わった名前ですが、環の一種のようです。環で発生する零因子による困った問題を排除しています。
- 整域(乗法モノイドである必要がある)
- 零が唯一の零因子: a * x = 0かつa != 0ならばx = 0
- 非自明環: 自明環(零のみの集合は {0} 環となるので、自明環と呼ばれる)ではない
力尽きた
群環体の「体」まで辿り着きたかったのですが、整閉整域、一意分解整域、主イデアル整域、ユークリッド整域、体、有限体、と訳のわからない名前のオンパレードで、力尽きました。また今度調べます。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月16日
一般のご家庭にPCは何台ある?
目次: PC
内閣府の「主要耐久消費財等の普及率」「主要耐久消費財の保有数量の推移」(リンク)によると、2人以上の世帯のPC普及率は77.0%、100世帯辺り123.6台(2020年3月)だそうです。
保有世帯だけを考えれば123.6 / 0.77 / 100 = 1.61 [台/世帯] ですから、世帯人数 <PC台数です。PCを日常的に使う習慣がない限り、共有のPCが1台あれば十分ですし、納得感ある結果です。
一般のご家庭にPCは何台置ける?
では、一般のご家庭にPCは最大で何台置けるでしょうか?
PCの消費電力は様々ですが、夢はでっかく、高性能PCとして、AMD Threadripper 3990X, NVIDIA GeForce RTX 3090のマシンを考えましょう。CPUとグラボのTDPは280 + 350W = 630Wです。他の部品や損失を考えると、PC 1台あたり800W程度と思われます。
一般家庭の我が家の電気契約(40A)ですと、5台程度でブレーカーが飛びます。200V系のコンセントを増設し、200Vで給電すれば電流は半減するので10台くらいは置けるでしょう。30A契約のご家庭も多いでしょうから、「高性能PC 8〜10台」これが一般のご家庭の限界と思われます。
逸般の誤家庭にPCは何台置ける?
では、色々逸脱した逸般の誤家庭の場合はどうでしょうか?
家庭の電気契約は「従量電灯B」という契約(従量電灯B・C電気料金プラン - 東京電力エナジーパートナー株式会社)がほとんどです。従量電灯Bの最大契約アンペア数は60Aで、全て200Vから取ると最大12kWです。したがって12000 / 800 = 15台が限界です。ふーむ、意外と伸びませんね。
冷却の電力は完全に無視しています。冷却を無視したまま15台も置いたら、家の中は一瞬で灼熱地獄になり、人間もPCも死ぬと思います。
業務用なら青天井
大口需要向けに「従量電灯C」という契約もあります。
従量電灯Cの場合10Aごとに基本料金が従量的に増える青天井の契約になります。一般家庭でも契約可能のようです。基本料金を比較すると、従量電灯B< 従量電灯Cとなるため、一般のご家庭だと損するだけで契約する意味はありません。
本来、家電が大量にある豪邸や、業務用の電気機器がある商店用ですが、60Aに満足できない真の逸般の誤家庭にも向いているかもしれませんね。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月25日
Slideshare初利用
Slideshareを初めて使いました。LinkedInのアカウントが必要なのは知りませんでした。偶然LinkedInのアカウントを持っていたので、すんなり登録できました。
USB PDはもっとわかりやすくしてほしい
試しに USB Type-C, USB PDケーブルとお友達になろうをアップロードしました。ダウンロードもできるし、スライド置き場として優秀ですね。みんな使うわけだ……。
スライドの話もしておくと、USB Type-Cケーブルがどうして何種類もあって、値段が全然違うのか、気になったので調べたことをまとめたものです。USB初心者なので間違ってたらすみません。
最後まで分からなかったのはUSB Power Deliveryの3A/5Aケーブルを見分ける方法です。何か無いんでしょうか。当然USB PDのアナライザで見ればわかりますよ?でもアナライザなんか普通の人は持ってませんよ。パッケージから出した途端に見分けが付かなくなるなんて、一般消費者からしてみたら辛すぎません?
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月27日
新キーボードMajestouch購入
目次: PC
先日の在宅勤務環境改善(2021年2月12日の日記参照)にて、デュアルディスプレイにしたところ、ノートPC本体が邪魔になってしまったので、机の上からどけました。
当然、ThinkPad本体のキーボードには手が届きませんから、ワイヤレスキーボードLogicool K295を買いました。Amazonで1,900円くらいでした。K295は変なキーも少ないし、静かで良いですが、キーの認識が渋いです。私の場合、打鍵力が足りず人差し指担当のキー(T, Uなど)の誤打が多発してイライラします。
買ってすぐ買い替えるのもどうかと悩みましたけど、あまりに誤打が多く慣れるまで辛そうだったので、さっさと諦めFILCOのMajestouch赤軸を買いました。ヨドバシで15,000円くらいでした。Majestouchはキーが戻るとき&底打ちしたとき「カーン!」と響く鐘のような音がやかましい以外は、非常に良いキーボードです。
キーボード使用歴
今まで、キーボードは標準的なキーボード(※)であれば、高くても安くても使い心地が気になることはないと思っていました。しかし今回K295がどうも合わなかったことから、実は自分とキーボードの相性って結構あるのか?と疑問に感じるようになりました。
(※)OADG 109A型の配列で、カーソルキー、ファンクションキー等の位置を移動していないキーボードのこと。
まずはキーボードの使用履歴を書き出してみます。
相性とか全く気にならなかった。
- DELLの標準キーボード
- Gatewayの標準キーボード
- HPの標準キーボード
- IBM/Lenovo ThinkPad X, Eシリーズ
- Logicool K270
- Majestouch赤軸
- NEC VersaPro
- Owltechの安いキーボード
- RealForce 108UBK
- サンワサプライの安いキーボード
- SONY VAIO Type-G
- TOSHIBA Dynabook R73
誤打しやすかった。
- Let's Noteシリーズ(理由: キーの形が横長)
- Logicool K295(理由: キーの認識が渋い)
- Logicool K340(理由: カーソル、ファンクションキー配置が変)
まともに打てなかった。
- HappyHacking(理由: キー配置が変すぎる)
以前K340やHHKで懲りて、特殊なキー配列のキーボードに触らなくなったので、コンパクト系のキーボードの利用歴はほぼゼロです。そもそもまともに打てないし、レビューできません。
ほとんどPC付属キーボード、ノートPCのキーボードばかりです。これはもしや、勝手に安物だと思いこんでいたPC付属の標準キーボード、実は質が高かったのではなかろうか?
大事な製品に標準で付属するものですし、高級ではないにせよ、あまりに変なものはつけませんよね。これが答えなのでは、という気がしてきました。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月28日
JIS配列キーボードとOADG配列キーボード
目次: PC
今まで、いわゆる日本語配列のキー配列のことを漠然とJIS配列と呼んでいましたが、どうもこれは正確ではないようです。
技術者たるもの、規格を粗末に扱ってはいけませんよね??
JIS配列を定めているのはJIS X 6002-1980「情報処理系けん盤配列」です。この配列を見ると一目瞭然ですが、アルファベット、スペースなどは一致するものの、他のキーは全く違う位置にあったり、そもそもなかったりします。規格書は有料(1,100円)ですが、PFUのサイトでJIS配列の図をタダで拝めます。
PFUのサイトへのリンク:
https://www.pfu.fujitsu.com/hhkeyboard/pfutechreview/section3.html
現状、主流の日本語キー配列はOADG(The PC Open Architecture Developers Group)が規格化した配列です。OADGは2004年に解散していますが、規格書はInternet Archiveで見ることができます。
Internet Archive: OADGテクニカル・リファレンス ハードウェア編1991年へのリンク:
https://archive.org/details/OADG1991/
規格の付録Aを見ると、
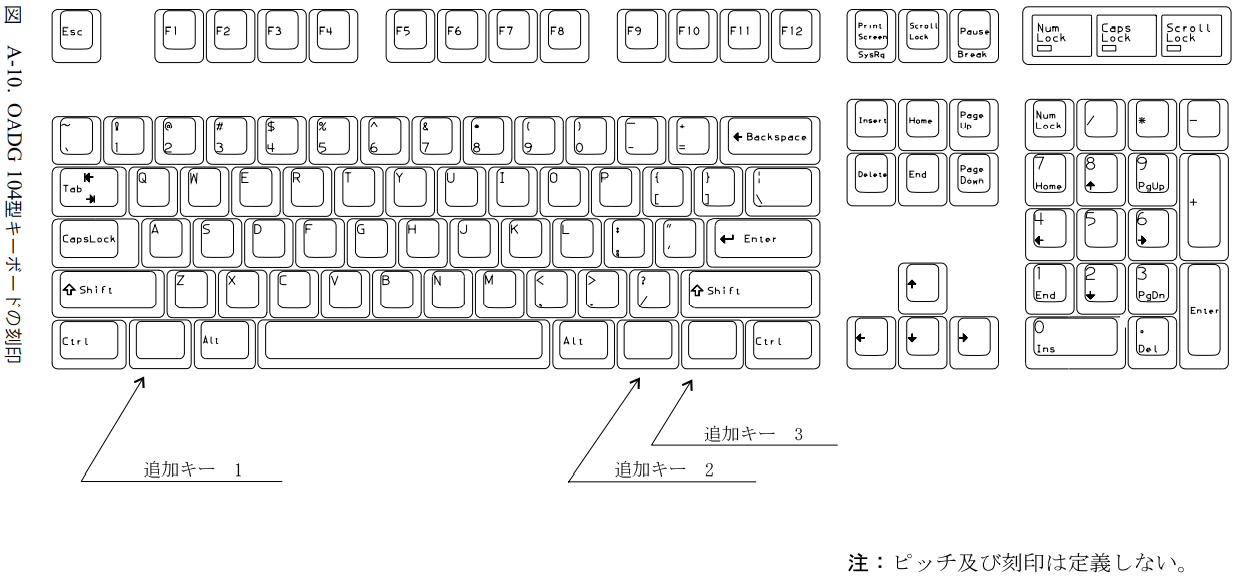
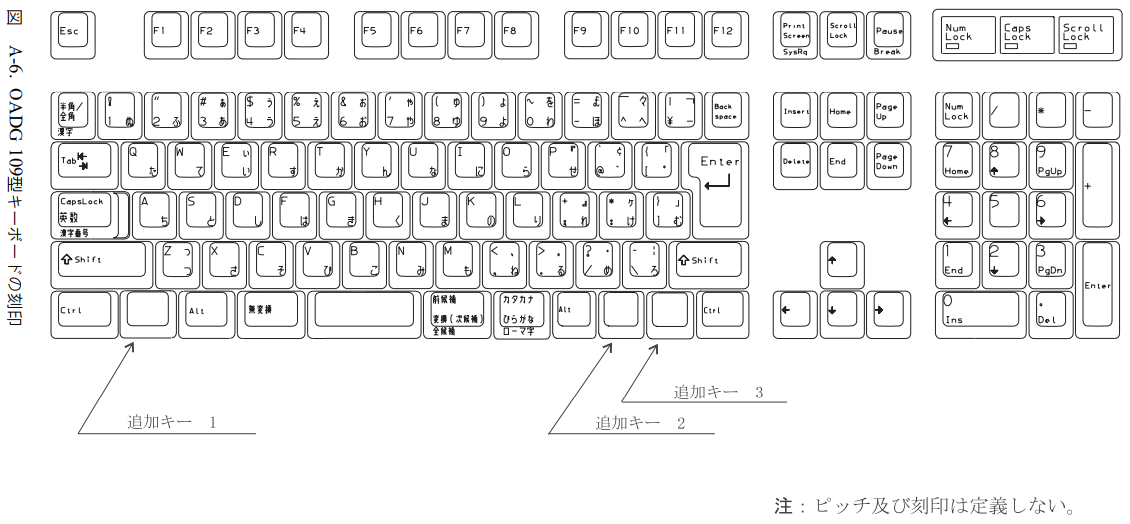
- OADG 104型(英語配列)
- OADG 109型(日本語配列)
- OADG 109A型(109型と同じだが、- や ^ キーの刻印が違う)
の3つが書かれています。市販のキーボードは、各社ともに適当に魔改造しているため、OADG規格と全く同じキー配列のキーボードは存在しないと思います。たぶん。
実例を出すと、Logicool K295はかなり109Aに近いです。しかし、右Windowsキーが欠けています(このタイプ、俗に108キーなどと呼ばれていますね)。
FILCO Majestouchも素直な109Aに近いですが、右Appキーがなく、右WindowsキーがFnキーに置換されています。

FILCO Majestouch Convertible 2のキー配列
私の場合は、最下段は 左Ctrl, 左Win, 左Alt, スペース, 右Alt, 右Ctrlしか使わないので、K295やMajestouchのように使わないキーが欠けていても気になりませんが、使う人からすると、何てことするの!?という気分になるでしょう。
さらに言うと、無変換、変換、ひらがなキーも使わないので、使っているキーの種類だけ考えたら、いわゆる英語配列(OADG 104型)で十分に思えます。しかし日本語配列で練習したため、英語配列は記号類を間違えまくります。私物で購入したことはありません。打てて損はないので、もうちょい修行しても良いかもしれませんね……?
メモ: 技術系の話はFacebookから転記しておくことにした。写真追加、加筆。
コメント一覧
- hdkさん(2021/03/05 21:43)
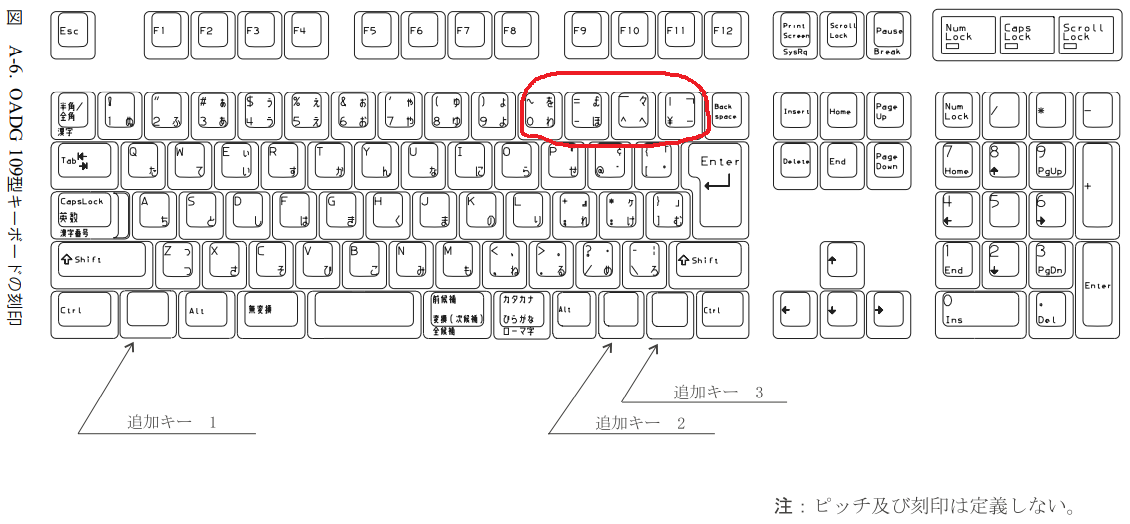
109と109Aって、かなの記号も違うんですよ。"P"のあたりにある"『""』"なんかがなくなっていますよね。勝手な想像では、主流のWindowsで入力できないから消しちゃったんだと思いますが... ThinkPadでいうとX20とX30のところで違いが見られるようです。
OADG誕生前のIBM JXではこのへんの記号も入力できていましたし、\と¥や〜と ̄が刻印どおりに区別されていました。(なおJXは英文モード対応の関係なのか、英語部分はUS配列だったので、位置が違いますが。) - すずきさん(2021/03/06 00:21)
ですね、その辺りも違います。違いを全部示すつもりはなかった(本文と関係ないし)のですが、下手に赤丸で囲ったのが良くなかったか……。
 この記事にコメントする
この記事にコメントする
こんてんつ
 wiki
wiki Linux JM
Linux JM Java API
Java API過去の日記
 2002年
2002年 2003年
2003年 2004年
2004年 2005年
2005年 2006年
2006年 2007年
2007年 2008年
2008年 2009年
2009年 2010年
2010年 2011年
2011年 2012年
2012年 2013年
2013年 2014年
2014年 2015年
2015年 2016年
2016年 2017年
2017年 2018年
2018年 2019年
2019年 2020年
2020年 2021年
2021年 2022年
2022年 2023年
2023年 2024年
2024年 2025年
2025年 2026年
2026年 過去日記について
過去日記についてその他の情報
 アクセス統計
アクセス統計 サーバ一覧
サーバ一覧 サイトの情報
サイトの情報