コグノスケ

未来から過去へ表示(*) link

過去から未来へ表示

もっと前

2014年11月15日 >>> 2014年11月2日

もっと後

2014年11月15日

permalink

編集する

USB-DACと矩形波

目次: PC

前回はSin波を見ました（2014年10月18日の日記参照）が、今回は矩形波を見てみようと思います。

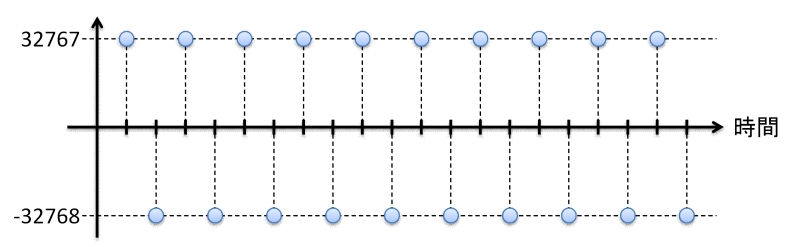
サンプリング周波数の1/2の周波数（以降、1/2 fsと書きます）の矩形波のLPCMデータを下記のように表すとします。

周波数1/2 fsの矩形波のLPCMデータ

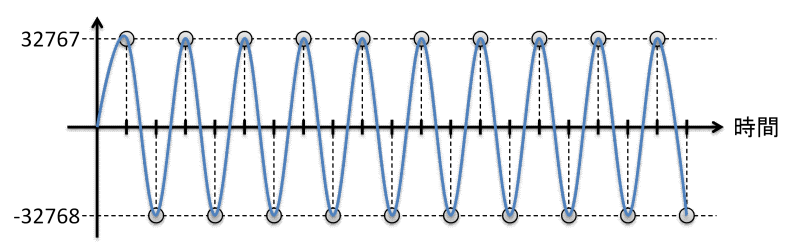
矩形波と書きましたが、このデータをアナログに変換しても矩形波にはなりません。下記のような22kHzのSin波になります。

周波数1/2 fsの矩形波をアナログに変換

私もそれほど詳しくはありませんが、標本化定理と言って、ある波形をサンプリング周波数44kHzでサンプリングした際に完全に元の波形に戻せるのは1/2 fs未満、つまり22kHzまでの周波数を持った波形です。それ以上は情報が失われ、元に戻せません。

見た目は周波数22kHzの波形に見える矩形波でも、波形の立上がり、立下りの部分に高い周波数を含んでいて、この部分が失われてしまうため、元に戻らないのです。

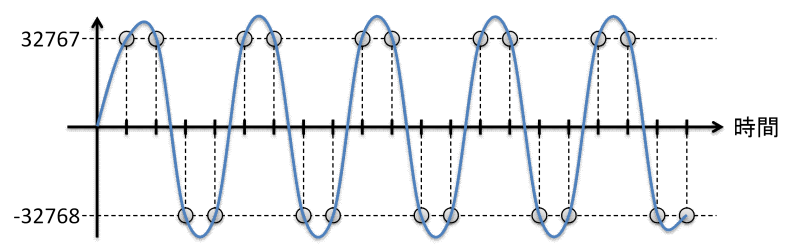
同じ理屈で1/4 fsの矩形波、つまり44kHzのサンプリング周波数で、11kHzの矩形波を表そうとしても、立上がり、立下りの部分が失われ、11kHzのSin波になります。LPCMデータの最大値は変わりませんが、22kHzの時より振幅が大きくなるのが面白いですね。

周波数1/4 fsの矩形波をアナログに変換

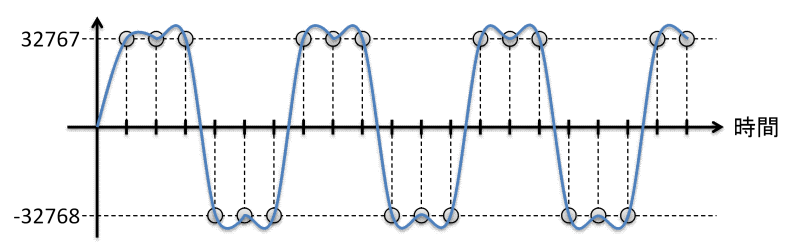
見た目が矩形波らしくなるのは1/6 fsか1/8 fsくらいでしょうか。つまり44kHzのサンプリング周波数で、7.4kHzか5.5kHzの矩形波を表そうとしたときです。

周波数1/6 fsの矩形波をアナログに変換

周波数1/8 fsの矩形波をアナログに変換

実際やってみましょう

では、下記のLPCMデータを使ってUSB-DACで再生してみます。

各種揃えましたが、訳あって、この中からサンプリング周波数44kHzのデータを使うことにします。まずは1/2 fsから。

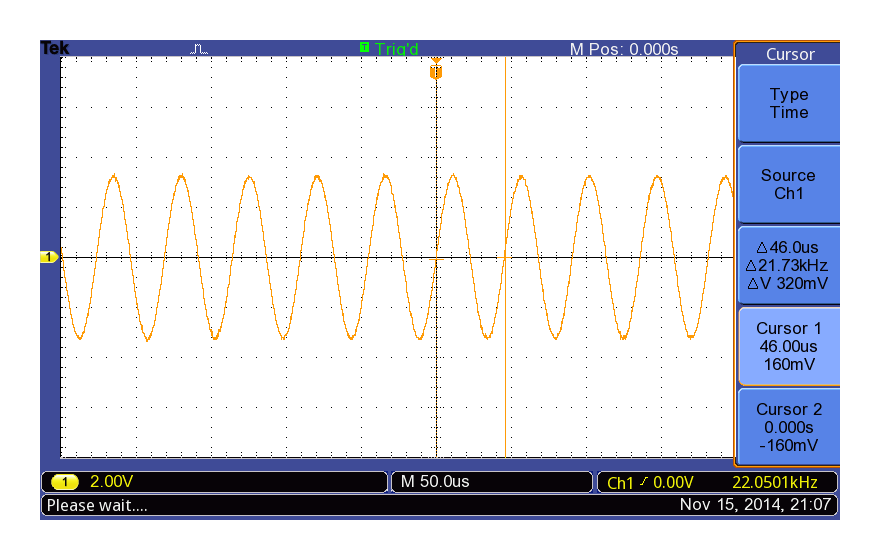
ONKYO SE-U33GXV2の22kHz矩形波出力（fs = 44.1kHz）

綺麗なSin波です。次は1/4 fsです。

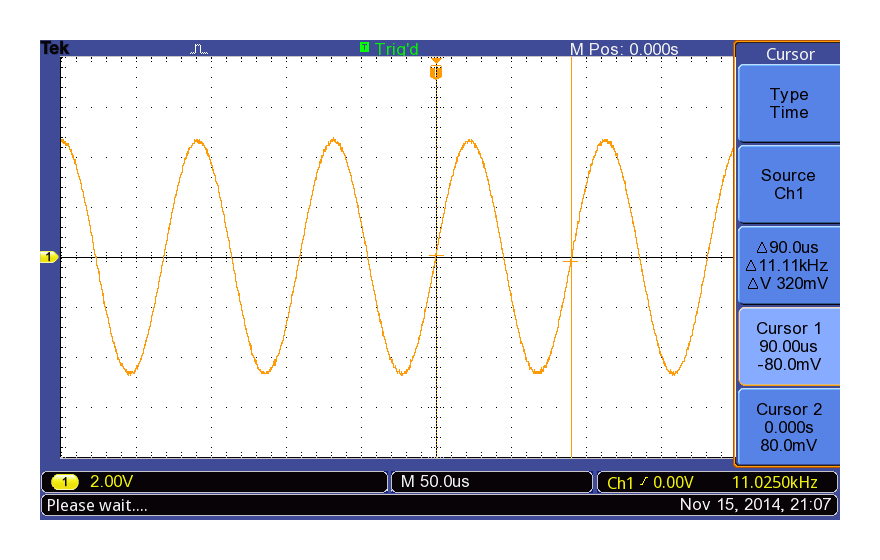
ONKYO SE-U33GXV2の11kHz矩形波出力（fs = 44.1kHz）

これも綺麗なSin波ですね。振幅が先ほどより大きいのがわかると思います。次は1/6 fsと1/8 fsです。

ONKYO SE-U33GXV2の7.4kHz矩形波出力（fs = 44.1kHz）

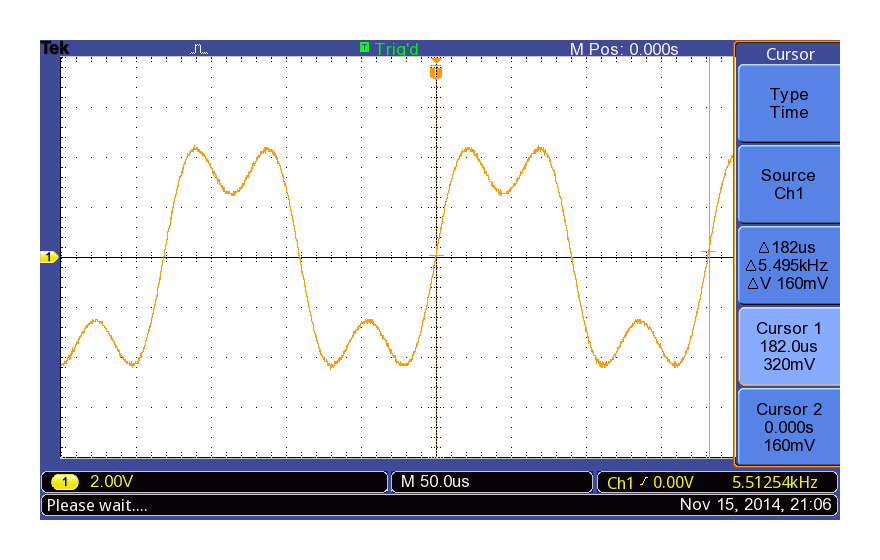
ONKYO SE-U33GXV2の5.5kHz矩形波出力（fs = 44.1kHz）

角の部分はまだガタガタしていますが、矩形波らしくなってきたのがわかります。

編集者:すずき(2024/10/25 02:03)

コメント一覧

すずきさん(2014/11/19 02:30)
DA 変換を調べていたら、どうも、図のような補完でリンギングが起きているわけではなさそうです。信号処理は難しいな…。

この記事にコメントする

もっと前

2014年11月15日 >>> 2014年11月2日

もっと後

管理用メニュー

記事を新規作成

RSSを更新

<	2014					>
<<	<	11			>	>>
日	月	火	水	木	金	土
-	-	-	-	-	-	1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	-	-	-	-	-	-

本日の日記へ

最近のコメント20件

21年9月20日
すずきさん (11/19 01:04)
「It was my pleasure.」
21年9月20日
whtさん (11/17 23:41)
「This blog solves my ...」
24年10月1日
すずきさん (10/06 03:41)
「xrdpで十分動作しているので、Wayl...」
24年10月1日
hdkさん (10/03 19:05)
「GNOMEをお使いでしたら今はWayla...」
24年10月1日
すずきさん (10/03 10:12)
「私は逆にVNCサーバーに繋ぐ使い方をした...」
24年10月1日
hdkさん (10/03 08:30)
「おー、面白いですね。xrdpはすでに立ち...」
14年6月13日
2048player...さん (09/26 01:04)
「最後に、この式を出すのに紙4枚(A4)も...」
14年6月13日
2048playerさん (09/26 01:00)
「今のところ最も簡略化した式です。\n--...」
14年6月13日
2048playerさん (09/16 01:00)
「返信ありがとうございます。\nコメントが...」
14年6月13日
すずきさん (09/12 21:19)
「コメントありがとうございます。同じ結果に...」
14年6月13日
2048playerさん (09/08 17:30)
「私も2048の最高スコアを求めたのですが...」
14年6月13日
2048さん (09/08 17:16)
「私も2048の最高スコアを求めたのですが...」
14年6月13日
2048playerさん (09/08 16:10)
「私も2048の最高スコアを求めたのですが...」
02年8月4日
lxbfYeaaさん (07/12 10:11)
「555」
24年6月17日
すずきさん (06/23 00:12)
「ありがとうございます。バルコニーではない...」
24年6月17日
hdkさん (06/22 22:08)
「GPSの最初の同期を取る時は見晴らしのい...」
24年5月16日
すずきさん (05/21 11:41)
「あー、確かにdpkg-reconfigu...」
24年5月16日
hdkさん (05/21 08:55)
「システム全体のlocale設定はDebi...」
24年5月17日
すずきさん (05/20 13:16)
「そうですねえ、普通はStandardなの...」
24年5月17日
hdkさん (05/19 07:45)
「なるほど、そういうことなんですね。Exc...」

もっとみる

こんてんつ

wiki

pukiwiki

Linux JM

Java API

Java 8

Java 7

Java 6

Java 2 SE 5.0
link

Java 2 SE 1.4.0
link

Java 2 SE 1.3
link

Java Media Framework 2.0

過去の日記

2002年

8月 9月
10月 11月 12月

2003年